Double integrator: time minimisation

The problem consists in minimising the final time $t_f$ for the double integrator system

\[ \dot x_1(t) = x_2(t), \quad \dot x_2(t) = u(t), \quad u(t) \in [-1,1],\]

and the limit conditions

\[ x(0) = (1,2), \quad x(t_f) = (0,0).\]

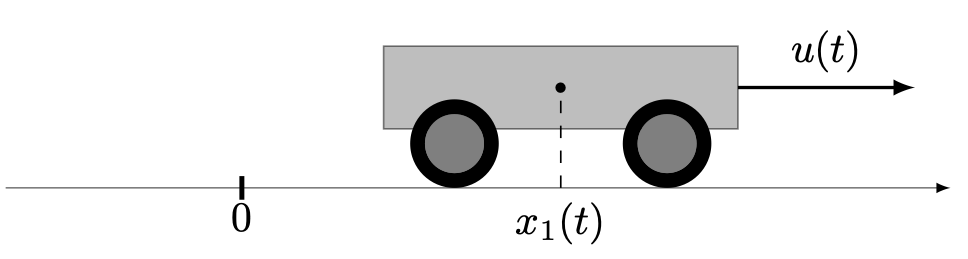
This problem can be interpretated as a simple model for a wagon with constant mass moving along a line without fricton.

First, we need to import the OptimalControl.jl package:

using OptimalControl

Then, we can define the problem

@def ocp begin
    tf ∈ R, variable
    t ∈ [ 0, tf ], time
    x ∈ R², state
    u ∈ R, control
    tf ≥ 0
    -1 ≤ u(t) ≤ 1
    q = x₁
    v = x₂
    q(0) == 1
    v(0) == 2
    q(tf) == 0
    v(tf) == 0
    0 ≤ q(t) ≤ 5,       (1)
    -2 ≤ v(t) ≤ 3,      (2)
    ẋ(t) == [ v(t), u(t) ]
    tf → min
end

Solve it

sol = solve(ocp)

Method = (:direct, :adnlp, :ipopt)
This is Ipopt version 3.14.14, running with linear solver MUMPS 5.6.2.

Number of nonzeros in equality constraint Jacobian...:     1004
Number of nonzeros in inequality constraint Jacobian.:        0
Number of nonzeros in Lagrangian Hessian.............:      202

Total number of variables............................:      304
                     variables with only lower bounds:        1
                variables with lower and upper bounds:      303
                     variables with only upper bounds:        0
Total number of equality constraints.................:      204
Total number of inequality constraints...............:        0
        inequality constraints with only lower bounds:        0
   inequality constraints with lower and upper bounds:        0
        inequality constraints with only upper bounds:        0

iter    objective    inf_pr   inf_du lg(mu)  ||d||  lg(rg) alpha_du alpha_pr  ls
   0  1.0000000e-01 1.90e+00 0.00e+00   0.0 0.00e+00    -  0.00e+00 0.00e+00   0
   1  9.9999010e-04 1.88e+00 2.32e+01  -5.7 1.10e+01    -  8.53e-02 8.99e-03h  1
   2  9.9900010e-06 1.88e+00 6.44e+03  -5.7 1.84e+03    -  5.27e-04 1.07e-04h  1
   3r 9.9900010e-06 1.88e+00 9.99e+02   0.3 0.00e+00    -  0.00e+00 2.68e-07R  3
   4r 1.8899160e-03 1.74e+00 4.65e+02  -0.7 4.77e-01    -  4.73e-01 5.34e-01f  1
   5r 1.4658984e-01 1.73e+00 2.09e+01  -1.1 1.45e-01   2.0 9.79e-01 1.00e+00f  1
   6r 2.9193546e-01 1.70e+00 4.08e+01  -0.8 1.70e-01   2.4 1.00e+00 8.53e-01f  1
   7r 3.5836667e-01 1.70e+00 4.73e+01  -0.9 6.64e-02   2.9 1.00e+00 1.00e+00f  1
   8r 5.9834814e-01 1.70e+00 7.36e+01  -0.9 3.75e-01   2.4 9.65e-01 6.40e-01f  1
   9r 7.2398061e-01 1.70e+00 9.10e+01  -1.7 1.48e-01   2.8 1.00e+00 8.51e-01f  1
iter    objective    inf_pr   inf_du lg(mu)  ||d||  lg(rg) alpha_du alpha_pr  ls
  10r 8.4184963e-01 1.71e+00 4.59e+02  -1.7 6.10e-01   2.3 1.00e+00 1.93e-01f  1
  11r 9.4835839e-01 1.72e+00 7.81e+02  -1.3 3.80e-01   1.8 1.00e+00 2.80e-01f  1
  12r 1.0283813e+00 1.71e+00 8.78e+02  -1.6 5.91e-01   1.4 1.00e+00 1.67e-01f  1
  13r 1.0666091e+00 1.66e+00 2.42e+02  -2.8 1.71e-01   1.8 1.00e+00 5.19e-01f  1
  14  5.7360280e-01 1.56e+00 5.29e+01   0.3 1.05e+01    -  2.58e-01 6.17e-02h  1
  15  6.1993703e-01 1.56e+00 7.19e+01  -5.7 4.08e+02    -  2.38e-03 2.47e-03h  1
  16  7.2554684e-01 1.55e+00 7.04e+01  -5.7 1.98e+02    -  6.46e-03 2.79e-03h  1
  17  9.7142594e-01 1.53e+00 5.07e+01  -5.7 6.37e+01    -  1.85e-02 1.07e-02h  1
  18  1.6662909e+00 1.45e+00 1.50e+01   0.5 1.28e+01    -  1.10e-01 5.58e-02f  1
  19  7.3295731e+00 1.70e-01 4.17e+02   0.3 6.42e+00    -  6.24e-01 8.83e-01f  1
iter    objective    inf_pr   inf_du lg(mu)  ||d||  lg(rg) alpha_du alpha_pr  ls
  20  6.1520840e+00 1.78e-02 1.48e+02   0.1 1.41e+00    -  1.00e+00 9.21e-01h  1
  21  6.2752208e+00 2.09e-04 1.72e+01  -0.5 2.95e-01    -  9.95e-01 9.90e-01f  1
  22  6.2660417e+00 1.86e-06 6.24e+00  -2.2 1.23e-02    -  1.00e+00 9.91e-01h  1
  23  5.6695137e+00 1.84e-03 2.90e-02  -2.8 5.97e-01    -  1.00e+00 1.00e+00f  1
  24  5.5118889e+00 7.92e-04 6.45e+02  -3.3 5.19e-01    -  9.78e-01 1.00e+00h  1
  25  5.4861365e+00 1.97e-04 6.37e+03  -3.8 5.63e-01    -  1.00e+00 8.15e-01h  1
  26  5.4663359e+00 4.94e-05 6.71e+01  -4.8 5.00e-01    -  1.00e+00 9.97e-01h  1
  27  5.4649557e+00 7.68e-08 1.39e-07  -5.8 6.24e-03    -  1.00e+00 1.00e+00h  1
  28  5.4648096e+00 1.42e-09 3.60e-01 -11.0 1.33e-03    -  9.97e-01 1.00e+00h  1
  29  5.4648096e+00 4.44e-16 3.99e-16 -10.3 1.55e-06    -  1.00e+00 1.00e+00h  1

Number of Iterations....: 29

                                   (scaled)                 (unscaled)
Objective...............:   5.4648095606409361e+00    5.4648095606409361e+00
Dual infeasibility......:   3.9885413453548932e-16    3.9885413453548932e-16
Constraint violation....:   4.4408920985006262e-16    4.4408920985006262e-16
Variable bound violation:   9.5654382192833509e-09    9.5654382192833509e-09
Complementarity.........:   5.0382564513651442e-11    5.0382564513651442e-11
Overall NLP error.......:   5.0382564513651442e-11    5.0382564513651442e-11


Number of objective function evaluations             = 34
Number of objective gradient evaluations             = 21
Number of equality constraint evaluations            = 34
Number of inequality constraint evaluations          = 0
Number of equality constraint Jacobian evaluations   = 31
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations             = 29
Total seconds in IPOPT                               = 0.585

EXIT: Optimal Solution Found.

and plot the solution

plot(sol, size=(600, 450))