Numerical developments to solve optimal control problems in Julia

rewrite in OptimalControl.jl DSL the free time problem below as a problem with fixed final time using:
- a change time from t to s = t / tf
- tf as an additional state variable subject to dtf / ds = 0
ocp = @def begin
    tf ∈ R,          variable
    t ∈ [0, tf],     time
    x = (q, v) ∈ R², state
    u ∈ R,           control
    -1 ≤ u(t) ≤ 1
    q(0)  == -1
    v(0)  == 0
    q(tf) == 0
    v(tf) == 0
    ẋ(t) == [v(t), u(t)]
    tf → min
end

ocp_fixed = @def begin
    # Fixed time domain
    s ∈ [0, 1], time
    
    # Augmented state: (position, velocity, final_time)
    y = (q, v, tf) ∈ R³, state
    
    # Control
    u ∈ R, control
    
    # Transformed dynamics (multiply by tf due to ds = dt/tf)
    ∂(q)(s)  == tf(s) * v(s)
    ∂(v)(s)  == tf(s) * u(s)
    ∂(tf)(s) == 0
    
    # Initial conditions
    q(0)  == -1
    v(0)  == 0
    # tf(0) is free (no initial condition needed)
    
    # Final conditions
    q(1)  == 0
    v(1)  == 0
    # tf(1) is what we minimize
    
    # Control constraints
    -1 ≤ u(s) ≤ 1
    
    # Cost: minimize final time
    tf(1) → min
end

This is MadNLP version v0.8.7, running with cuDSS v0.4.0

Number of nonzeros in constraint Jacobian............:    12005
Number of nonzeros in Lagrangian Hessian.............:     9000

Total number of variables............................:     4004
                     variables with only lower bounds:        0
                variables with lower and upper bounds:        0
                     variables with only upper bounds:        0
Total number of equality constraints.................:     3005
Total number of inequality constraints...............:        0
        inequality constraints with only lower bounds:        0
   inequality constraints with lower and upper bounds:        0
        inequality constraints with only upper bounds:        0

iter    objective    inf_pr   inf_du lg(mu)  ||d||  lg(rg) alpha_du alpha_pr  ls
   0  1.0000000e-01 1.10e+00 1.00e+00  -1.0 0.00e+00    -  0.00e+00 0.00e+00   0
   1  1.0001760e-01 1.10e+00 3.84e-03  -1.0 6.88e+02  -4.0 1.00e+00 2.00e-07h  2
   2 -5.2365072e-03 1.89e-02 1.79e-07  -1.0 6.16e+00  -4.5 1.00e+00 1.00e+00h  1
   3  5.9939621e+00 2.28e-03 1.66e-04  -3.8 6.00e+00  -5.0 9.99e-01 1.00e+00h  1
   4  5.9996210e+00 2.94e-06 8.38e-07  -3.8 7.70e-02    -  1.00e+00 1.00e+00h  1

Number of Iterations....: 4

                                   (scaled)                 (unscaled)
Objective...............:   5.9996210189633494e+00    5.9996210189633494e+00
Dual infeasibility......:   8.3756005011360529e-07    8.3756005011360529e-07
Constraint violation....:   2.9426923277963834e-06    2.9426923277963834e-06
Complementarity.........:   2.0007459547789288e-06    2.0007459547789288e-06
Overall NLP error.......:   2.9426923277963834e-06    2.9426923277963834e-06

Number of objective function evaluations             = 6
Number of objective gradient evaluations             = 5
Number of constraint evaluations                     = 6
Number of constraint Jacobian evaluations            = 5
Number of Lagrangian Hessian evaluations             = 4
Total wall-clock secs in solver (w/o fun. eval./lin. alg.)  =  0.072
Total wall-clock secs in linear solver                      =  0.008
Total wall-clock secs in NLP function evaluations           =  0.003
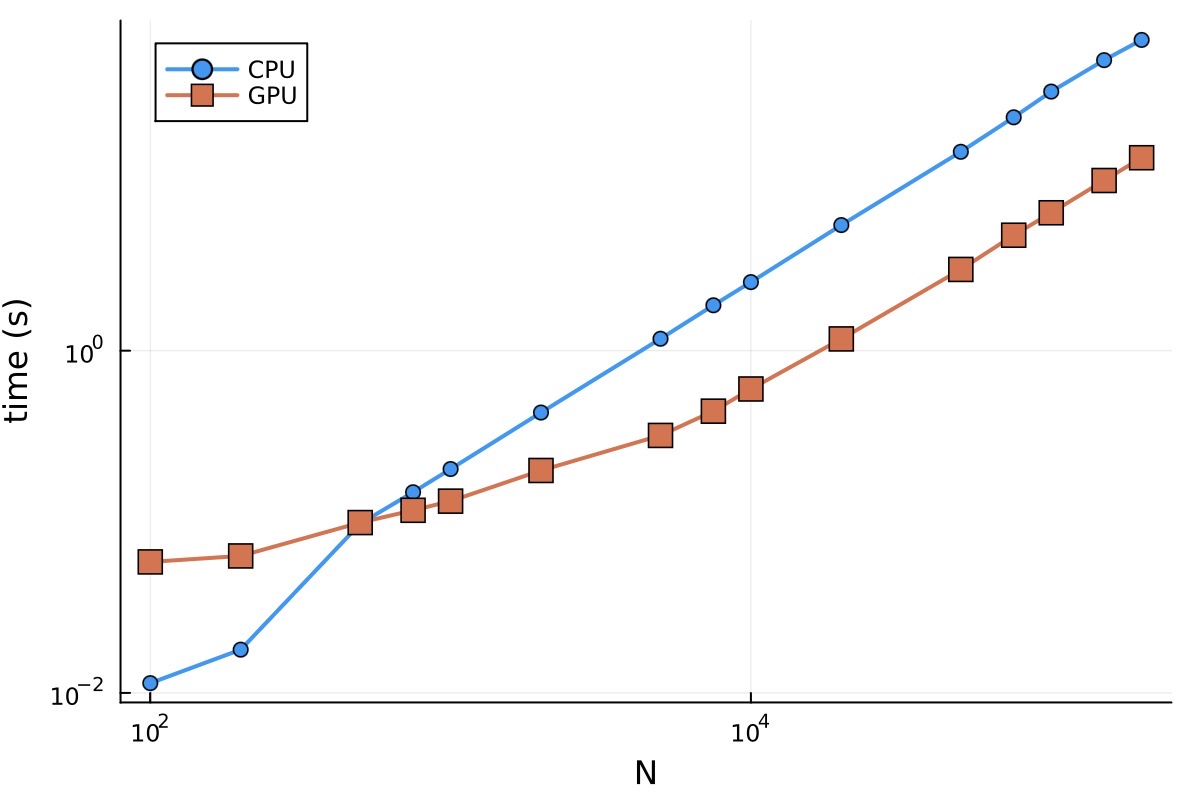
Total wall-clock secs                                       =  0.083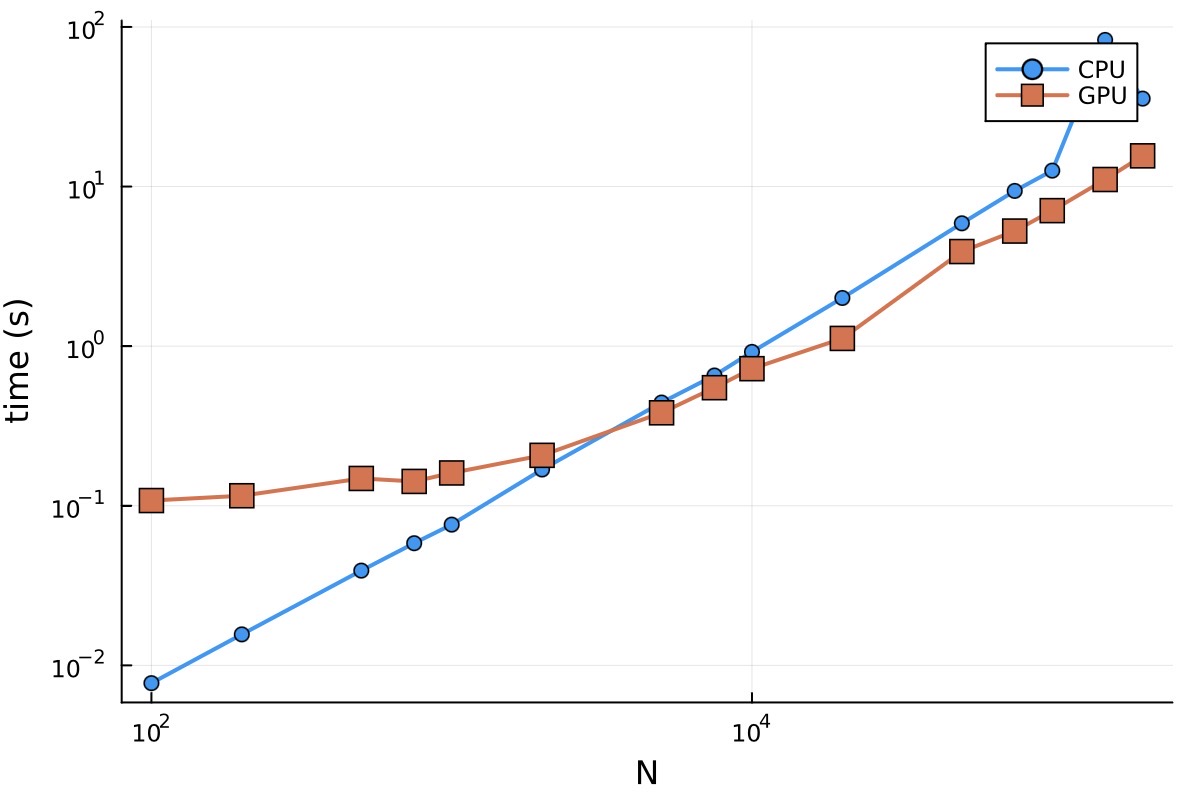

• Mini-benchmark: Goddard and Quadrotor problems
• Goddard, H100 run

• Quadrotor, H100 run