GitHub

Minimum time orbit transfer

Introduction

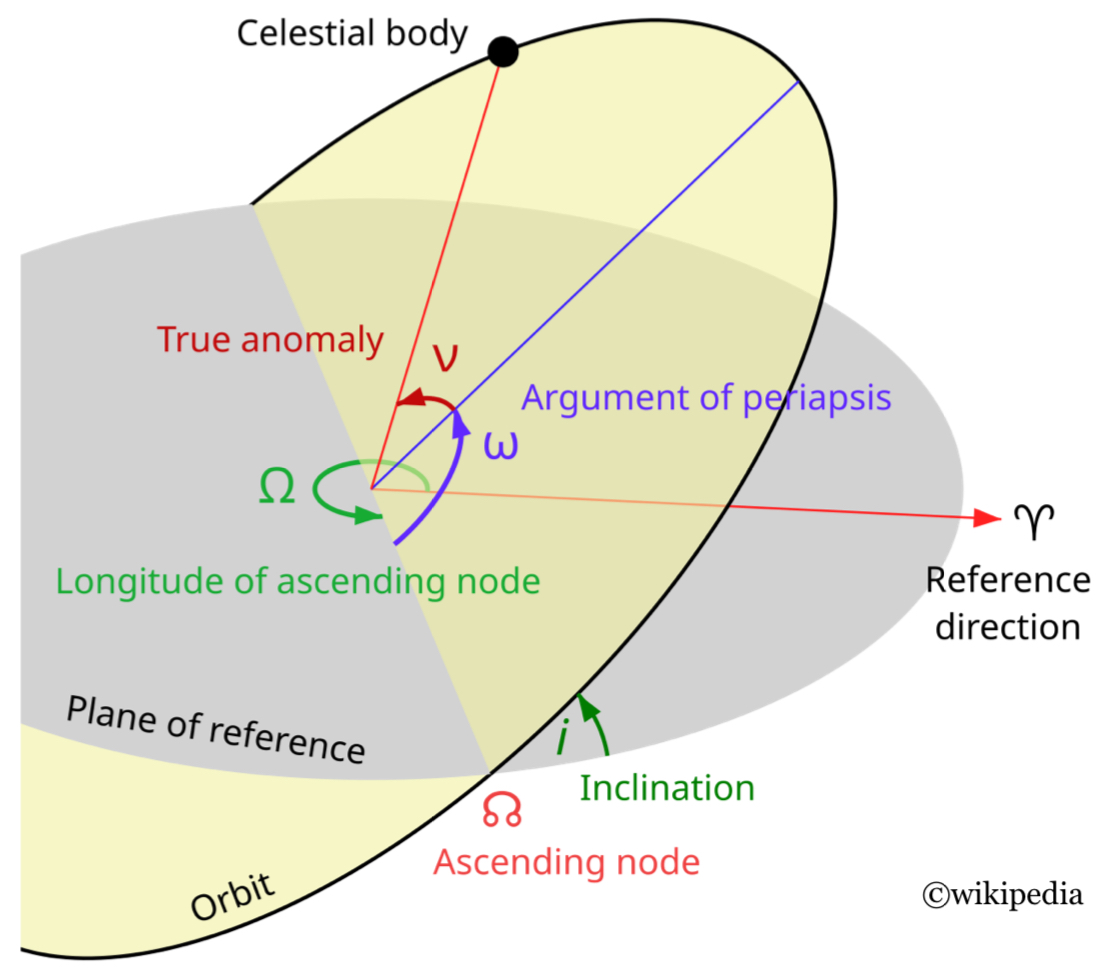
Minimum time control of the Kepler equation (CNES / TAS / Inria / CNRS collaboration, check [1] and [2]):

\[\begin{cases} t_f \to \min,\\ \ddot{q} = -\mu\frac{q}{|q|^3} + \frac{u}{m}\,,\quad t \in [0,t_f],\\ \dot{m} = -\beta|u|,\quad |u| \leq T_{\mathrm{max}}. \end{cases}\]

Fixed initial and final Keplerian orbits (free final longitude).

using OptimalControl
using NLPModelsIpopt
using OrdinaryDiffEq
using Plots
using MINPACK
using ForwardDiff
using LinearAlgebra

Problem definition

Tmax = 60                                  # Maximum thrust in Newtons
cTmax = 3600^2 / 1e6; T = Tmax * cTmax     # Conversion from Newtons to kg x Mm / h²
mass0 = 1500                               # Initial mass of the spacecraft
β = 1.42e-02                               # Engine specific impulsion
μ = 5165.8620912                           # Earth gravitation constant
P0 = 11.625                                # Initial semilatus rectum
ex0, ey0 = 0.75, 0                         # Initial eccentricity
hx0, hy0 = 6.12e-2, 0                      # Initial ascending node and inclination
L0 = π                                     # Initial longitude
Pf = 42.165                                # Final semilatus rectum
exf, eyf = 0, 0                            # Final eccentricity
hxf, hyf = 0, 0                            # Final ascending node and inclination

asqrt(x; ε=1e-9) = sqrt(sqrt(x^2+ε^2))     # Avoid issues with AD

function F0(x)
    P, ex, ey, hx, hy, L = x
    pdm = asqrt(P / μ)
    cl = cos(L)
    sl = sin(L)
    w = 1 + ex * cl + ey * sl
    F = zeros(eltype(x), 6) # Use eltype to allow overloading for AD
    F[6] = w^2 / (P * pdm)
    return F
end

function F1(x)
    P, ex, ey, hx, hy, L = x
    pdm = asqrt(P / μ)
    cl = cos(L)
    sl = sin(L)
    F = zeros(eltype(x), 6)
    F[2] = pdm *   sl
    F[3] = pdm * (-cl)
    return F
end

function F2(x)
    P, ex, ey, hx, hy, L = x
    pdm = asqrt(P / μ)
    cl = cos(L)
    sl = sin(L)
    w = 1 + ex * cl + ey * sl
    F = zeros(eltype(x), 6)
    F[1] = pdm * 2 * P / w
    F[2] = pdm * (cl + (ex + cl) / w)
    F[3] = pdm * (sl + (ey + sl) / w)
    return F
end

function F3(x)
    P, ex, ey, hx, hy, L = x
    pdm = asqrt(P / μ)
    cl = cos(L)
    sl = sin(L)
    w = 1 + ex * cl + ey * sl
    pdmw = pdm / w
    zz = hx * sl - hy * cl
    uh = (1 + hx^2 + hy^2) / 2
    F = zeros(eltype(x), 6)
    F[2] = pdmw * (-zz * ey)
    F[3] = pdmw *   zz * ex
    F[4] = pdmw *   uh * cl
    F[5] = pdmw *   uh * sl
    F[6] = pdmw *   zz
    return F
end

Direct solve

tf = 15                                      # Estimation of final time
Lf = 3π                                      # Estimation of final longitude
x0 = [P0, ex0, ey0, hx0, hy0, L0]            # Initial state
xf = [Pf, exf, eyf, hxf, hyf, Lf]            # Final state
x(t) = x0 + (xf - x0) * t / tf               # Linear interpolation
u = [0.1, 0.5, 0.]                        # Initial guess for the control
nlp_init = (state=x, control=u, variable=tf) # Initial guess for the NLP

ocp = @def begin
    tf ∈ R, variable
    t ∈ [0, tf], time
    x = (P, ex, ey, hx, hy, L) ∈ R⁶, state
    u ∈ R³, control
    x(0) == x0
    x[1:5](tf) == xf[1:5]
    mass = mass0 - β * T * t
    ẋ(t) == F0(x(t)) + T / mass * (u₁(t) * F1(x(t)) + u₂(t) * F2(x(t)) + u₃(t) * F3(x(t)))
    u₁(t)^2 + u₂(t)^2 + u₃(t)^2 ≤ 1
    tf → min
end
    tf ∈ R, variable
    t ∈ [0, tf], time
    x = ((P, ex, ey, hx, hy, L) ∈ R⁶, state)
    u ∈ R³, control
    x(0) == x0
    (x[1:5])(tf) == xf[1:5]
    mass = mass0 - β * T * t
    ẋ(t) == F0(x(t)) + (T / mass) * (u₁(t) * F1(x(t)) + u₂(t) * F2(x(t)) + u₃(t) * F3(x(t)))
    u₁(t) ^ 2 + u₂(t) ^ 2 + u₃(t) ^ 2 ≤ 1
    tf → min

The optimal control problem is of the form:

    minimize  J(x, u, tf) = g(x(0), x(tf), tf)

    subject to

        ẋ(t) = f(t, x(t), u(t), tf), t in [0, tf] a.e.,

        ψ₋ ≤ ψ(t, x(t), u(t), tf) ≤ ψ₊, 
        ϕ₋ ≤ ϕ(x(0), x(tf), tf) ≤ ϕ₊, 

    where x(t) = (P(t), ex(t), ey(t), hx(t), hy(t), L(t)) ∈ R⁶, u(t) ∈ R³ and tf ∈ R.

Declarations (* required):
╭────────┬────────┬──────────┬──────────┬───────────┬────────────┬─────────────╮
│ times* │ state* │ control* │ variable │ dynamics* │ objective* │ constraints │
├────────┼────────┼──────────┼──────────┼───────────┼────────────┼─────────────┤
│   V    │   V    │    V     │    V     │     V     │     V      │      V      │
╰────────┴────────┴──────────┴──────────┴───────────┴────────────┴─────────────╯

nlp_sol = OptimalControl.solve(ocp; init=nlp_init, grid_size=100)
This is Ipopt version 3.14.17, running with linear solver MUMPS 5.7.3.

Number of nonzeros in equality constraint Jacobian...:    11011
Number of nonzeros in inequality constraint Jacobian.:      303
Number of nonzeros in Lagrangian Hessian.............:     4445

Total number of variables............................:      910
                     variables with only lower bounds:        0
                variables with lower and upper bounds:        0
                     variables with only upper bounds:        0
Total number of equality constraints.................:      611
Total number of inequality constraints...............:      101
        inequality constraints with only lower bounds:        0
   inequality constraints with lower and upper bounds:        0
        inequality constraints with only upper bounds:      101

iter    objective    inf_pr   inf_du lg(mu)  ||d||  lg(rg) alpha_du alpha_pr  ls
   0  1.5000000e+01 2.14e-01 2.46e-01   0.0 0.00e+00    -  0.00e+00 0.00e+00   0
   1  1.5632877e+01 1.73e-01 6.59e-01  -6.1 7.27e+00    -  5.95e-01 1.90e-01h  3
   2  1.6096872e+01 1.51e-01 1.15e+00  -6.4 3.71e+00   0.0 4.78e-01 1.25e-01h  4
   3  1.9018883e+01 6.12e-02 2.70e+00  -1.1 3.97e+00  -0.5 7.39e-01 6.03e-01H  1
   4  2.0358419e+01 1.56e-02 1.98e+00  -1.7 1.60e+00  -0.1 1.00e+00 8.38e-01h  1
   5  2.0617233e+01 2.68e-04 4.98e-01  -3.6 2.59e-01   0.4 1.00e+00 1.00e+00h  1
   6  2.0429778e+01 3.01e-04 1.53e-01  -3.7 1.87e-01  -0.1 1.00e+00 1.00e+00h  1
   7  1.9857419e+01 2.52e-03 1.52e-01  -4.6 5.72e-01  -0.6 1.00e+00 1.00e+00f  1
   8  1.9319499e+01 5.35e-03 1.22e-01  -2.7 1.03e+00  -1.1 1.00e+00 5.20e-01f  1
   9  1.8399038e+01 4.64e-02 7.26e-02  -2.4 1.40e+00  -1.5 1.00e+00 6.59e-01f  1
iter    objective    inf_pr   inf_du lg(mu)  ||d||  lg(rg) alpha_du alpha_pr  ls
  10  1.7193105e+01 3.05e+00 2.62e-01  -2.1 3.01e+00  -2.0 1.00e+00 8.31e-01f  1
  11  1.5106279e+01 1.10e+01 3.82e-01  -2.2 1.36e+01  -2.5 1.70e-01 3.23e-01h  1
  12  1.5675085e+01 2.15e+00 2.08e-01  -2.2 1.62e+00  -1.2 7.98e-01 1.00e+00h  1
  13  1.5767117e+01 1.59e-01 7.09e-02  -2.2 7.59e-01  -0.7 1.00e+00 1.00e+00h  1
  14  1.5167619e+01 5.39e-01 1.06e-01  -1.9 6.62e+00    -  1.00e+00 4.46e-01h  1
  15  1.5207976e+01 1.55e-01 2.60e-01  -2.2 1.87e+00    -  1.00e+00 7.88e-01h  1
  16  1.4958081e+01 2.78e-02 2.02e-02  -4.0 4.59e-01    -  1.00e+00 9.93e-01h  1
  17  1.5012097e+01 4.19e-01 7.47e-03  -2.5 6.61e-01    -  1.00e+00 9.34e-01h  1
  18  1.4993570e+01 2.41e-04 5.76e-04  -2.7 3.51e-01    -  1.00e+00 1.00e+00h  1
  19  1.4814517e+01 9.34e-04 3.26e-03  -8.7 2.05e-01    -  1.00e+00 1.00e+00h  1
iter    objective    inf_pr   inf_du lg(mu)  ||d||  lg(rg) alpha_du alpha_pr  ls
  20  1.4796807e+01 5.17e-04 5.95e-05  -5.1 6.84e-02    -  1.00e+00 1.00e+00h  1
  21  1.4796405e+01 1.26e-07 1.37e-08 -11.0 1.93e-03    -  1.00e+00 1.00e+00h  1

Number of Iterations....: 21

                                   (scaled)                 (unscaled)
Objective...............:   1.4796404863783373e+01    1.4796404863783373e+01
Dual infeasibility......:   1.3697506295873296e-08    1.3697506295873296e-08
Constraint violation....:   1.2616821831734626e-07    1.2616821831734626e-07
Variable bound violation:   0.0000000000000000e+00    0.0000000000000000e+00
Complementarity.........:   1.3417720767463476e-08    1.3417720767463476e-08
Overall NLP error.......:   1.2616821831734626e-07    1.2616821831734626e-07


Number of objective function evaluations             = 33
Number of objective gradient evaluations             = 22
Number of equality constraint evaluations            = 33
Number of inequality constraint evaluations          = 33
Number of equality constraint Jacobian evaluations   = 22
Number of inequality constraint Jacobian evaluations = 22
Number of Lagrangian Hessian evaluations             = 21
Total seconds in IPOPT                               = 6.251

EXIT: Optimal Solution Found.
tf = variable(nlp_sol)
p  = costate(nlp_sol)
p0 = p(0)
plot(nlp_sol)
Example block output

Shooting (1/2), Tmax = 60 Newtons

function ur(x, p, tf) # Regular maximising control
    H1 = p' * F1(x)
    H2 = p' * F2(x)
    H3 = p' * F3(x)
    u = [H1, H2, H3]
    u = u / sqrt(u[1]^2 + u[2]^2 + u[3]^2)
    return u
end

fr = Flow(ocp, ur) # Regular flow (first version)

function shoot(ξ::Vector{T}) where T
    tf, p0 = ξ[1], ξ[2:end]
    xf_, pf = fr(0, x0, p0, tf)
    s = zeros(T, 7)
    s[1:5] = xf_[1:5] - xf[1:5]
    s[6] = pf[6]
    s[7] = p0[1]^2 + p0[2]^2 + p0[3]^2 + p0[4]^2 + p0[5]^2 + p0[6]^2 - 1
    return s
end

p0 = p0 / norm(p0) # Normalization |p0|=1 for free final time
ξ = [tf; p0]; # Initial guess
jshoot(ξ) = ForwardDiff.jacobian(shoot, ξ)
shoot!(s, ξ) = (s[:] = shoot(ξ); nothing)
jshoot!(js, ξ) = (js[:] = jshoot(ξ); nothing)
bvp_sol = fsolve(shoot!, jshoot!, ξ; show_trace=true); println(bvp_sol)
Iter     f(x) inf-norm    Step 2-norm      Step time
------   --------------   --------------   --------------
     1     1.441506e+00     0.000000e+00         7.911273
     2     7.828904e-02     5.822092e-05        14.433610
     3     1.805789e-02     1.793255e-05         0.006112
     4     4.039623e-03     6.129907e-07         0.005667
     5     1.138619e-04     1.107407e-08         0.015535
     6     6.538025e-05     1.359255e-10         0.005620
     7     6.244845e-06     4.489006e-12         0.009841
     8     3.534559e-08     5.342350e-14         0.005779
     9     3.606218e-10     1.853859e-18         0.008501
Results of Nonlinear Solver Algorithm
 * Algorithm: Modified Powell (User Jac, Expert)
 * Starting Point: [14.796404863783373, -0.016164433702769165, -0.9050962222165153, -0.3306787679250943, -0.09648293225364692, 0.035148118586239945, 0.24626559970809675]
 * Zero: [14.800364354664758, -0.016189714921626915, -0.9084889547974425, -0.3252598589830436, -0.09447217088704539, 0.03432296283542438, 0.24184432891069754]
 * Inf-norm of residuals: 0.000000
 * Convergence: true
 * Message: algorithm estimates that the relative error between x and the solution is at most tol
 * Total time: 22.402010 seconds
 * Function Calls: 9
 * Jacobian Calls (df/dx): 1

Shooting (2/2), Tmax = 0.7 Newtons

hr = (t, x, p) -> begin # Regular maximised Hamiltonian (more efficient)
    H0 = p' * F0(x)
    H1 = p' * F1(x)
    H2 = p' * F2(x)
    H3 = p' * F3(x)
    mass = mass0 - β*T*t
    h = H0 + T / mass * sqrt(H1^2 + H2^2 + H3^2)
    return h
end

hr = Hamiltonian(hr; autonomous=false)
fr = Flow(hr) # Regular flow (again)

Tmax = 0.7                                 # Maximum thrust (Newtons)
cTmax = 3600^2 / 1e6; T = Tmax * cTmax     # Conversion from Newtons to kg x Mm / h²
tf = 1.210e3; p0 =-[-2.215319700438820e+01, -4.347109477345140e+01, 9.613188807286992e-01, 3.181800985503019e+02, -2.307236094862410e+00, -5.797863110671591e-01] # Tmax = 0.7 Newtons
p0 = p0 / norm(p0) # Normalization |p0|=1 for free final time
ξ = [tf; p0]; # Initial guess

bvp_sol = fsolve(shoot!, jshoot!, ξ; show_trace=true); println(bvp_sol)
Iter     f(x) inf-norm    Step 2-norm      Step time
------   --------------   --------------   --------------
     1     1.073118e+00     0.000000e+00         4.371657
     2     1.431619e-01     1.222060e+01        11.056950
     3     1.090263e-01     1.104500e+01         0.289040
     4     1.847681e-02     2.971575e+00         0.317280
     5     1.996342e-02     4.468500e-01         0.262949
     6     8.607891e-03     2.181855e-02         0.293898
     7     2.826201e-03     2.618597e-03         0.267660
     8     1.241794e-03     7.993872e-05         0.293262
     9     1.555157e-03     6.602970e-05         0.289012
    10     7.599961e-05     2.809120e-05         0.290977
    11     4.206481e-05     1.773353e-07         0.297937
    12     7.672444e-06     3.852977e-07         0.275044
    13     5.441236e-07     7.260827e-09         0.265315
    14     5.909087e-08     4.510506e-11         0.380645
    15     2.813787e-08     2.110683e-13         0.664074
    16     4.440955e-09     3.591076e-17         0.345580
Results of Nonlinear Solver Algorithm
 * Algorithm: Modified Powell (User Jac, Expert)
 * Starting Point: [1210.0, 0.06881811251625697, 0.13504139789537645, -0.0029863026489984875, -0.9884150724670144, 0.007167346236588738, 0.001801085395597836]
 * Zero: [1214.5922195529836, 0.06933409656211512, 0.5161919854246422, -0.0002316690086500129, -0.8536506970530086, 0.004363238004614628, -9.327820837705058e-5]
 * Inf-norm of residuals: 0.000000
 * Convergence: true
 * Message: algorithm estimates that the relative error between x and the solution is at most tol
 * Total time: 19.961381 seconds
 * Function Calls: 16
 * Jacobian Calls (df/dx): 1

Plots

tf = bvp_sol.x[1]
p0 = bvp_sol.x[2:end]
ode_sol = fr((0, tf), x0, p0)
t  = ode_sol.t; N = size(t, 1)
P  = ode_sol[1, :]
ex = ode_sol[2, :]
ey = ode_sol[3, :]
hx = ode_sol[4, :]
hy = ode_sol[5, :]
L  = ode_sol[6, :]
cL = cos.(L)
sL = sin.(L)
w  = @. 1 + ex * cL + ey * sL
Z  = @. hx * sL - hy * cL
C  = @. 1 + hx^2 + hy^2
q1 = @. P *((1 + hx^2 - hy^2) * cL + 2 * hx * hy * sL) / (C * w)
q2 = @. P *((1 - hx^2 + hy^2) * sL + 2 * hx * hy * cL) / (C * w)
q3 = @. 2 * P * Z / (C * w)

plt1 = plot3d(1; xlim = (-60, 60), ylim = (-60, 60), zlim = (-5, 5), title = "Orbit transfer", legend=false)
@gif for i = 1:N
    push!(plt1, q1[i], q2[i], q3[i])
end every N ÷ min(N, 100)
Example block output

Reproducibility

The documentation of this package was built using these direct dependencies,
Status `~/work/Kepler.jl/Kepler.jl/docs/Project.toml`
  [e30172f5] Documenter v1.10.1
⌅ [f6369f11] ForwardDiff v0.10.38
  [459d104a] Kepler v0.2.0 `~/work/Kepler.jl/Kepler.jl`
  [4854310b] MINPACK v1.3.0
  [f4238b75] NLPModelsIpopt v0.10.4
  [5f98b655] OptimalControl v1.0.0
  [1dea7af3] OrdinaryDiffEq v6.93.0
  [91a5bcdd] Plots v1.40.13
  [37e2e46d] LinearAlgebra v1.11.0
Info Packages marked with ⌅ have new versions available but compatibility constraints restrict them from upgrading. To see why use `status --outdated`
and using this machine and Julia version.
Julia Version 1.11.5
Commit 760b2e5b739 (2025-04-14 06:53 UTC)
Build Info:
  Official https://julialang.org/ release
Platform Info:
  OS: Linux (x86_64-linux-gnu)
  CPU: 4 × AMD EPYC 7763 64-Core Processor
  WORD_SIZE: 64
  LLVM: libLLVM-16.0.6 (ORCJIT, znver3)
Threads: 1 default, 0 interactive, 1 GC (on 4 virtual cores)
Environment:
  JULIA_PKG_SERVER_REGISTRY_PREFERENCE = eager
A more complete overview of all dependencies and their versions is also provided.
Status `~/work/Kepler.jl/Kepler.jl/docs/Manifest.toml`
  [54578032] ADNLPModels v0.8.12
  [47edcb42] ADTypes v1.14.0
  [a4c015fc] ANSIColoredPrinters v0.0.1
  [1520ce14] AbstractTrees v0.4.5
  [7d9f7c33] Accessors v0.1.42
  [79e6a3ab] Adapt v4.3.0
  [66dad0bd] AliasTables v1.1.3
  [ec485272] ArnoldiMethod v0.4.0
  [4fba245c] ArrayInterface v7.18.0
  [4c555306] ArrayLayouts v1.11.1
  [13072b0f] AxisAlgorithms v1.1.0
  [6e4b80f9] BenchmarkTools v1.6.0
  [d1d4a3ce] BitFlags v0.1.9
  [62783981] BitTwiddlingConvenienceFunctions v0.1.6
  [70df07ce] BracketingNonlinearSolve v1.1.3
  [2a0fbf3d] CPUSummary v0.2.6
⌅ [54762871] CTBase v0.15.0
  [790bbbee] CTDirect v0.14.8
  [1c39547c] CTFlows v0.8.1
  [34c4fa32] CTModels v0.2.3
  [32681960] CTParser v0.2.3
  [d360d2e6] ChainRulesCore v1.25.1
  [fb6a15b2] CloseOpenIntervals v0.1.13
  [523fee87] CodecBzip2 v0.8.5
  [944b1d66] CodecZlib v0.7.8
  [35d6a980] ColorSchemes v3.29.0
  [3da002f7] ColorTypes v0.12.1
  [c3611d14] ColorVectorSpace v0.11.0
  [5ae59095] Colors v0.13.0
  [38540f10] CommonSolve v0.2.4
  [bbf7d656] CommonSubexpressions v0.3.1
  [f70d9fcc] CommonWorldInvalidations v1.0.0
  [34da2185] Compat v4.16.0
  [a33af91c] CompositionsBase v0.1.2
  [2569d6c7] ConcreteStructs v0.2.3
  [f0e56b4a] ConcurrentUtilities v2.5.0
  [187b0558] ConstructionBase v1.5.8
  [d38c429a] Contour v0.6.3
  [adafc99b] CpuId v0.3.1
  [a8cc5b0e] Crayons v4.1.1
  [9a962f9c] DataAPI v1.16.0
  [864edb3b] DataStructures v0.18.22
  [e2d170a0] DataValueInterfaces v1.0.0
  [8bb1440f] DelimitedFiles v1.9.1
  [2b5f629d] DiffEqBase v6.167.2
  [163ba53b] DiffResults v1.1.0
  [b552c78f] DiffRules v1.15.1
  [a0c0ee7d] DifferentiationInterface v0.6.52
  [ffbed154] DocStringExtensions v0.9.4
  [e30172f5] Documenter v1.10.1
  [4e289a0a] EnumX v1.0.5
  [f151be2c] EnzymeCore v0.8.8
  [460bff9d] ExceptionUnwrapping v0.1.11
  [d4d017d3] ExponentialUtilities v1.27.0
  [e2ba6199] ExprTools v0.1.10
  [55351af7] ExproniconLite v0.10.14
  [c87230d0] FFMPEG v0.4.2
  [7034ab61] FastBroadcast v0.3.5
  [9aa1b823] FastClosures v0.3.2
  [442a2c76] FastGaussQuadrature v1.0.2
  [a4df4552] FastPower v1.1.2
  [1a297f60] FillArrays v1.13.0
  [6a86dc24] FiniteDiff v2.27.0
  [53c48c17] FixedPointNumbers v0.8.5
  [1fa38f19] Format v1.3.7
⌅ [f6369f11] ForwardDiff v0.10.38
  [069b7b12] FunctionWrappers v1.1.3
  [77dc65aa] FunctionWrappersWrappers v0.1.3
  [46192b85] GPUArraysCore v0.2.0
  [28b8d3ca] GR v0.73.14
  [c145ed77] GenericSchur v0.5.5
  [d7ba0133] Git v1.3.1
  [86223c79] Graphs v1.12.1
  [42e2da0e] Grisu v1.0.2
  [34c5aeac] HSL v0.5.0
  [cd3eb016] HTTP v1.10.16
  [b5f81e59] IOCapture v0.2.5
  [615f187c] IfElse v0.1.1
  [d25df0c9] Inflate v0.1.5
  [a98d9a8b] Interpolations v0.15.1
  [3587e190] InverseFunctions v0.1.17
  [b6b21f68] Ipopt v1.9.0
  [92d709cd] IrrationalConstants v0.2.4
  [82899510] IteratorInterfaceExtensions v1.0.0
  [1019f520] JLFzf v0.1.11
  [692b3bcd] JLLWrappers v1.7.0
  [682c06a0] JSON v0.21.4
  [0f8b85d8] JSON3 v1.14.2
  [ae98c720] Jieko v0.2.1
  [459d104a] Kepler v0.2.0 `~/work/Kepler.jl/Kepler.jl`
  [ba0b0d4f] Krylov v0.10.0
  [b964fa9f] LaTeXStrings v1.4.0
  [23fbe1c1] Latexify v0.16.7
  [10f19ff3] LayoutPointers v0.1.17
  [0e77f7df] LazilyInitializedFields v1.3.0
  [5078a376] LazyArrays v2.6.1
  [87fe0de2] LineSearch v0.1.4
  [d3d80556] LineSearches v7.3.0
  [5c8ed15e] LinearOperators v2.10.0
  [7ed4a6bd] LinearSolve v3.8.0
  [2ab3a3ac] LogExpFunctions v0.3.29
  [e6f89c97] LoggingExtras v1.1.0
  [4854310b] MINPACK v1.3.0
  [33e6dc65] MKL v0.8.0
  [d8e11817] MLStyle v0.4.17
  [1914dd2f] MacroTools v0.5.16
  [d125e4d3] ManualMemory v0.1.8
  [d0879d2d] MarkdownAST v0.1.2
  [b8f27783] MathOptInterface v1.39.0
  [bb5d69b7] MaybeInplace v0.1.4
  [739be429] MbedTLS v1.1.9
  [442fdcdd] Measures v0.3.2
  [e1d29d7a] Missings v1.2.0
  [2e0e35c7] Moshi v0.3.5
  [46d2c3a1] MuladdMacro v0.2.4
  [d8a4904e] MutableArithmetics v1.6.4
  [a4795742] NLPModels v0.21.4
  [f4238b75] NLPModelsIpopt v0.10.4
  [d41bc354] NLSolversBase v7.9.1
  [77ba4419] NaNMath v1.1.3
  [8913a72c] NonlinearSolve v4.6.0
  [be0214bd] NonlinearSolveBase v1.5.3
  [5959db7a] NonlinearSolveFirstOrder v1.3.1
  [9a2c21bd] NonlinearSolveQuasiNewton v1.2.1
  [26075421] NonlinearSolveSpectralMethods v1.1.1
  [6fe1bfb0] OffsetArrays v1.17.0
  [4d8831e6] OpenSSL v1.4.3
  [5f98b655] OptimalControl v1.0.0
  [bac558e1] OrderedCollections v1.8.0
  [1dea7af3] OrdinaryDiffEq v6.93.0
  [89bda076] OrdinaryDiffEqAdamsBashforthMoulton v1.2.0
  [6ad6398a] OrdinaryDiffEqBDF v1.4.0
  [bbf590c4] OrdinaryDiffEqCore v1.22.0
  [50262376] OrdinaryDiffEqDefault v1.3.0
  [4302a76b] OrdinaryDiffEqDifferentiation v1.6.0
  [9286f039] OrdinaryDiffEqExplicitRK v1.1.0
  [e0540318] OrdinaryDiffEqExponentialRK v1.4.0
  [becaefa8] OrdinaryDiffEqExtrapolation v1.5.0
  [5960d6e9] OrdinaryDiffEqFIRK v1.10.0
  [101fe9f7] OrdinaryDiffEqFeagin v1.1.0
  [d3585ca7] OrdinaryDiffEqFunctionMap v1.1.1
  [d28bc4f8] OrdinaryDiffEqHighOrderRK v1.1.0
  [9f002381] OrdinaryDiffEqIMEXMultistep v1.3.0
  [521117fe] OrdinaryDiffEqLinear v1.1.0
  [1344f307] OrdinaryDiffEqLowOrderRK v1.2.0
  [b0944070] OrdinaryDiffEqLowStorageRK v1.3.0
  [127b3ac7] OrdinaryDiffEqNonlinearSolve v1.6.0
  [c9986a66] OrdinaryDiffEqNordsieck v1.1.0
  [5dd0a6cf] OrdinaryDiffEqPDIRK v1.3.0
  [5b33eab2] OrdinaryDiffEqPRK v1.1.0
  [04162be5] OrdinaryDiffEqQPRK v1.1.0
  [af6ede74] OrdinaryDiffEqRKN v1.1.0
  [43230ef6] OrdinaryDiffEqRosenbrock v1.9.0
  [2d112036] OrdinaryDiffEqSDIRK v1.3.0
  [669c94d9] OrdinaryDiffEqSSPRK v1.2.1
  [e3e12d00] OrdinaryDiffEqStabilizedIRK v1.3.0
  [358294b1] OrdinaryDiffEqStabilizedRK v1.1.0
  [fa646aed] OrdinaryDiffEqSymplecticRK v1.3.0
  [b1df2697] OrdinaryDiffEqTsit5 v1.1.0
  [79d7bb75] OrdinaryDiffEqVerner v1.1.1
  [65ce6f38] PackageExtensionCompat v1.0.2
  [d96e819e] Parameters v0.12.3
  [69de0a69] Parsers v2.8.2
  [ccf2f8ad] PlotThemes v3.3.0
  [995b91a9] PlotUtils v1.4.3
  [91a5bcdd] Plots v1.40.13
  [f517fe37] Polyester v0.7.16
  [1d0040c9] PolyesterWeave v0.2.2
  [d236fae5] PreallocationTools v0.4.26
⌅ [aea7be01] PrecompileTools v1.2.1
  [21216c6a] Preferences v1.4.3
  [08abe8d2] PrettyTables v2.4.0
  [43287f4e] PtrArrays v1.3.0
  [be4d8f0f] Quadmath v0.5.11
  [c84ed2f1] Ratios v0.4.5
  [3cdcf5f2] RecipesBase v1.3.4
  [01d81517] RecipesPipeline v0.6.12
  [731186ca] RecursiveArrayTools v3.31.2
  [189a3867] Reexport v1.2.2
  [2792f1a3] RegistryInstances v0.1.0
  [05181044] RelocatableFolders v1.0.1
  [ae029012] Requires v1.3.1
  [37e2e3b7] ReverseDiff v1.16.1
  [7e49a35a] RuntimeGeneratedFunctions v0.5.13
  [94e857df] SIMDTypes v0.1.0
  [0bca4576] SciMLBase v2.84.0
  [19f34311] SciMLJacobianOperators v0.1.2
  [c0aeaf25] SciMLOperators v0.3.13
  [53ae85a6] SciMLStructures v1.7.0
  [6c6a2e73] Scratch v1.2.1
  [efcf1570] Setfield v1.1.2
  [992d4aef] Showoff v1.0.3
  [777ac1f9] SimpleBufferStream v1.2.0
  [727e6d20] SimpleNonlinearSolve v2.2.2
  [699a6c99] SimpleTraits v0.9.4
  [ce78b400] SimpleUnPack v1.1.0
  [ff4d7338] SolverCore v0.3.8
  [a2af1166] SortingAlgorithms v1.2.1
  [9f842d2f] SparseConnectivityTracer v0.6.17
  [47a9eef4] SparseDiffTools v2.24.0
  [0a514795] SparseMatrixColorings v0.4.18
  [276daf66] SpecialFunctions v2.5.1
  [860ef19b] StableRNGs v1.0.2
  [aedffcd0] Static v1.2.0
  [0d7ed370] StaticArrayInterface v1.8.0
  [90137ffa] StaticArrays v1.9.13
  [1e83bf80] StaticArraysCore v1.4.3
  [10745b16] Statistics v1.11.1
  [82ae8749] StatsAPI v1.7.0
  [2913bbd2] StatsBase v0.34.4
  [7792a7ef] StrideArraysCore v0.5.7
  [892a3eda] StringManipulation v0.4.1
  [856f2bd8] StructTypes v1.11.0
  [2efcf032] SymbolicIndexingInterface v0.3.39
  [3783bdb8] TableTraits v1.0.1
  [bd369af6] Tables v1.12.0
  [62fd8b95] TensorCore v0.1.1
  [8290d209] ThreadingUtilities v0.5.3
  [a759f4b9] TimerOutputs v0.5.28
  [3bb67fe8] TranscodingStreams v0.11.3
  [781d530d] TruncatedStacktraces v1.4.0
  [5c2747f8] URIs v1.5.2
  [3a884ed6] UnPack v1.0.2
  [1cfade01] UnicodeFun v0.4.1
  [1986cc42] Unitful v1.22.0
  [45397f5d] UnitfulLatexify v1.6.4
  [41fe7b60] Unzip v0.2.0
  [19fa3120] VertexSafeGraphs v0.2.0
  [efce3f68] WoodburyMatrices v1.0.0
  [ae81ac8f] ASL_jll v0.1.3+0
  [6e34b625] Bzip2_jll v1.0.9+0
⌃ [83423d85] Cairo_jll v1.18.4+0
  [ee1fde0b] Dbus_jll v1.16.2+0
  [2702e6a9] EpollShim_jll v0.0.20230411+1
  [2e619515] Expat_jll v2.6.5+0
⌅ [b22a6f82] FFMPEG_jll v4.4.4+1
  [a3f928ae] Fontconfig_jll v2.16.0+0
  [d7e528f0] FreeType2_jll v2.13.4+0
  [559328eb] FriBidi_jll v1.0.17+0
  [0656b61e] GLFW_jll v3.4.0+2
  [d2c73de3] GR_jll v0.73.14+0
  [78b55507] Gettext_jll v0.21.0+0
  [f8c6e375] Git_jll v2.49.0+0
⌃ [7746bdde] Glib_jll v2.82.4+0
  [3b182d85] Graphite2_jll v1.3.15+0
  [017b0a0e] HSL_jll v4.0.2+0
  [2e76f6c2] HarfBuzz_jll v8.5.0+0
  [e33a78d0] Hwloc_jll v2.12.0+0
  [1d5cc7b8] IntelOpenMP_jll v2025.0.4+0
  [9cc047cb] Ipopt_jll v300.1400.1700+0
  [aacddb02] JpegTurbo_jll v3.1.1+0
  [c1c5ebd0] LAME_jll v3.100.2+0
  [88015f11] LERC_jll v4.0.1+0
  [1d63c593] LLVMOpenMP_jll v18.1.7+0
  [dd4b983a] LZO_jll v2.10.3+0
⌅ [e9f186c6] Libffi_jll v3.2.2+2
  [7e76a0d4] Libglvnd_jll v1.7.1+1
  [94ce4f54] Libiconv_jll v1.18.0+0
  [4b2f31a3] Libmount_jll v2.41.0+0
  [89763e89] Libtiff_jll v4.7.1+0
  [38a345b3] Libuuid_jll v2.41.0+0
  [d00139f3] METIS_jll v5.1.3+0
  [856f044c] MKL_jll v2025.0.1+1
  [d7ed1dd3] MUMPS_seq_jll v500.700.301+0
  [e7412a2a] Ogg_jll v1.3.5+1
  [656ef2d0] OpenBLAS32_jll v0.3.29+0
  [458c3c95] OpenSSL_jll v3.0.16+0
  [efe28fd5] OpenSpecFun_jll v0.5.6+0
  [91d4177d] Opus_jll v1.3.3+0
  [36c8627f] Pango_jll v1.56.1+0
  [30392449] Pixman_jll v0.44.2+0
⌅ [c0090381] Qt6Base_jll v6.7.1+1
⌅ [629bc702] Qt6Declarative_jll v6.7.1+2
⌅ [ce943373] Qt6ShaderTools_jll v6.7.1+1
⌃ [e99dba38] Qt6Wayland_jll v6.7.1+1
⌅ [319450e9] SPRAL_jll v2024.5.8+0
  [a44049a8] Vulkan_Loader_jll v1.3.243+0
⌃ [a2964d1f] Wayland_jll v1.21.0+2
  [2381bf8a] Wayland_protocols_jll v1.36.0+0
⌅ [02c8fc9c] XML2_jll v2.13.6+1
  [ffd25f8a] XZ_jll v5.8.1+0
  [f67eecfb] Xorg_libICE_jll v1.1.2+0
  [c834827a] Xorg_libSM_jll v1.2.6+0
  [4f6342f7] Xorg_libX11_jll v1.8.12+0
  [0c0b7dd1] Xorg_libXau_jll v1.0.13+0
  [935fb764] Xorg_libXcursor_jll v1.2.3+0
  [a3789734] Xorg_libXdmcp_jll v1.1.6+0
  [1082639a] Xorg_libXext_jll v1.3.7+0
  [d091e8ba] Xorg_libXfixes_jll v6.0.1+0
  [a51aa0fd] Xorg_libXi_jll v1.8.2+0
  [d1454406] Xorg_libXinerama_jll v1.1.6+0
  [ec84b674] Xorg_libXrandr_jll v1.5.5+0
  [ea2f1a96] Xorg_libXrender_jll v0.9.12+0
  [c7cfdc94] Xorg_libxcb_jll v1.17.1+0
  [cc61e674] Xorg_libxkbfile_jll v1.1.3+0
  [e920d4aa] Xorg_xcb_util_cursor_jll v0.1.4+0
  [12413925] Xorg_xcb_util_image_jll v0.4.0+1
  [2def613f] Xorg_xcb_util_jll v0.4.0+1
  [975044d2] Xorg_xcb_util_keysyms_jll v0.4.0+1
  [0d47668e] Xorg_xcb_util_renderutil_jll v0.3.9+1
  [c22f9ab0] Xorg_xcb_util_wm_jll v0.4.1+1
  [35661453] Xorg_xkbcomp_jll v1.4.7+0
  [33bec58e] Xorg_xkeyboard_config_jll v2.39.0+0
  [c5fb5394] Xorg_xtrans_jll v1.6.0+0
  [3161d3a3] Zstd_jll v1.5.7+1
  [b792d7bf] cminpack_jll v1.3.12+0
  [35ca27e7] eudev_jll v3.2.9+0
  [214eeab7] fzf_jll v0.61.1+0
  [1a1c6b14] gperf_jll v3.1.1+1
  [a4ae2306] libaom_jll v3.11.0+0
  [0ac62f75] libass_jll v0.15.2+0
  [1183f4f0] libdecor_jll v0.2.2+0
  [2db6ffa8] libevdev_jll v1.11.0+0
  [f638f0a6] libfdk_aac_jll v2.0.3+0
  [36db933b] libinput_jll v1.18.0+0
  [b53b4c65] libpng_jll v1.6.47+0
  [f27f6e37] libvorbis_jll v1.3.7+2
  [009596ad] mtdev_jll v1.1.6+0
  [1317d2d5] oneTBB_jll v2022.0.0+0
⌅ [1270edf5] x264_jll v2021.5.5+0
⌅ [dfaa095f] x265_jll v3.5.0+0
  [d8fb68d0] xkbcommon_jll v1.4.1+2
  [0dad84c5] ArgTools v1.1.2
  [56f22d72] Artifacts v1.11.0
  [2a0f44e3] Base64 v1.11.0
  [ade2ca70] Dates v1.11.0
  [8ba89e20] Distributed v1.11.0
  [f43a241f] Downloads v1.6.0
  [7b1f6079] FileWatching v1.11.0
  [9fa8497b] Future v1.11.0
  [b77e0a4c] InteractiveUtils v1.11.0
  [4af54fe1] LazyArtifacts v1.11.0
  [b27032c2] LibCURL v0.6.4
  [76f85450] LibGit2 v1.11.0
  [8f399da3] Libdl v1.11.0
  [37e2e46d] LinearAlgebra v1.11.0
  [56ddb016] Logging v1.11.0
  [d6f4376e] Markdown v1.11.0
  [a63ad114] Mmap v1.11.0
  [ca575930] NetworkOptions v1.2.0
  [44cfe95a] Pkg v1.11.0
  [de0858da] Printf v1.11.0
  [9abbd945] Profile v1.11.0
  [3fa0cd96] REPL v1.11.0
  [9a3f8284] Random v1.11.0
  [ea8e919c] SHA v0.7.0
  [9e88b42a] Serialization v1.11.0
  [1a1011a3] SharedArrays v1.11.0
  [6462fe0b] Sockets v1.11.0
  [2f01184e] SparseArrays v1.11.0
  [f489334b] StyledStrings v1.11.0
  [fa267f1f] TOML v1.0.3
  [a4e569a6] Tar v1.10.0
  [8dfed614] Test v1.11.0
  [cf7118a7] UUIDs v1.11.0
  [4ec0a83e] Unicode v1.11.0
  [e66e0078] CompilerSupportLibraries_jll v1.1.1+0
  [deac9b47] LibCURL_jll v8.6.0+0
  [e37daf67] LibGit2_jll v1.7.2+0
  [29816b5a] LibSSH2_jll v1.11.0+1
  [c8ffd9c3] MbedTLS_jll v2.28.6+0
  [14a3606d] MozillaCACerts_jll v2023.12.12
  [4536629a] OpenBLAS_jll v0.3.27+1
  [05823500] OpenLibm_jll v0.8.5+0
  [efcefdf7] PCRE2_jll v10.42.0+1
  [bea87d4a] SuiteSparse_jll v7.7.0+0
  [83775a58] Zlib_jll v1.2.13+1
  [8e850b90] libblastrampoline_jll v5.11.0+0
  [8e850ede] nghttp2_jll v1.59.0+0
  [3f19e933] p7zip_jll v17.4.0+2
Info Packages marked with ⌃ and ⌅ have new versions available. Those with ⌃ may be upgradable, but those with ⌅ are restricted by compatibility constraints from upgrading. To see why use `status --outdated -m`

You can also download the manifest file and the project file.

References

  • 1Bonnard, B.; Caillau, J.-B.; Trélat, E. Geometric optimal control of elliptic Keplerian orbits. Discrete Contin. Dyn. Syst. Ser. B 5 (2005), no. 4, 929-956.
  • 2Caillau, J.-B.; Gergaud, J.; Noailles, J. 3D Geosynchronous Transfer of a Satellite: continuation on the Thrust. J. Optim. Theory Appl. 118 (2003), no. 3, 541-565.